Part 1: Fun With Filters
1.1: Finite Difference Operator
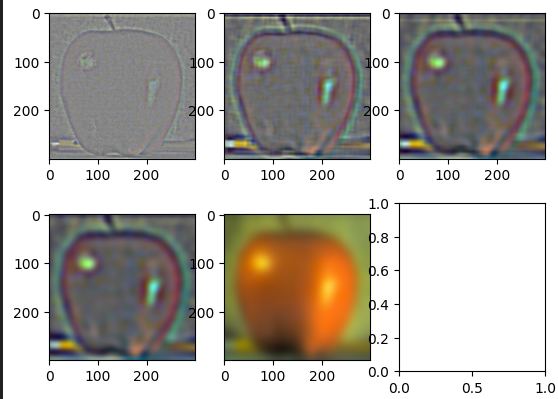
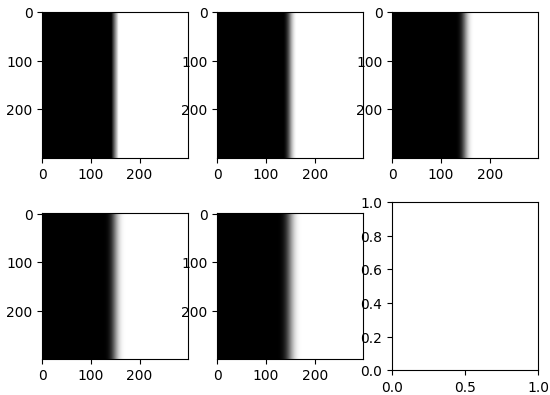
Below you can see the outputs from applying the finite difference operator to the cameraman image. This was done by convolving the cameramn image with the kernel [1, -1] to calculate the partial derivative with respect to x, and the kernel [[1], [-1]] to calculate the partial derivative with respect to y.


Finite difference gradients in x (left) and y (right)
Now we can use these 2 images to get the gradient magnitude image. To do this we did an elementwise transformation on both of these images. For each pixel I calculated grad_mag[i][j] = sqrt(dx[i][j]^2 + dy[i][j]^2). I then took these values along with a custom defined cutoff of 0.3 in order to binarize this image and successfully detect edges.


Gradient Magniutde Image (left) and Binarized Image (right)
1.2: Derivative of Gaussian
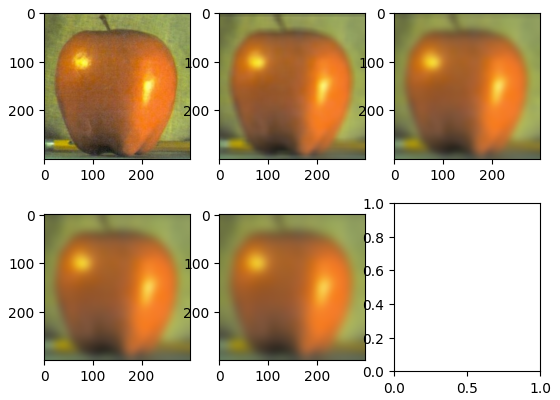
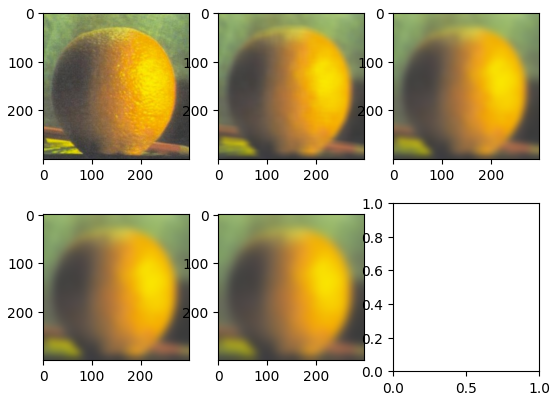
In order to improve the quality of the image derivatives that we are calculating we can use the derivative of gaussian filter. The filter works by first applying a gaussian blur low pass filter to remove the high frequency nosie from the image. This will smooth out the image and make the image gradients much more stable. After passing the image through the gaussian blur filter, we can then repeat the same finite difference operator convolution that we did in the previous part in order to generate a higher quality image gradient.



From left to right: Blurred Cameraman Image, Magnitude of Blurred Image Gradient, Thresholded Edge Detector
What differences do I See?
The biggest difference that I saw while doing this was that the gaussian edge detector was much better at gathering the full edge. In the normal edge detector, I had a lot of dots along the man's body and along the tripod. The detector wasn't able to pick up on all of the points along those edges, but in this there is a much better edge detection. Furthermore, the gradient magnitude image did a lot better job removing a lot of the edges along the grass. This is expected behavior because the grass is very high frequency data since there are a lot of small minimal edges that we don't necessarily want to detect.
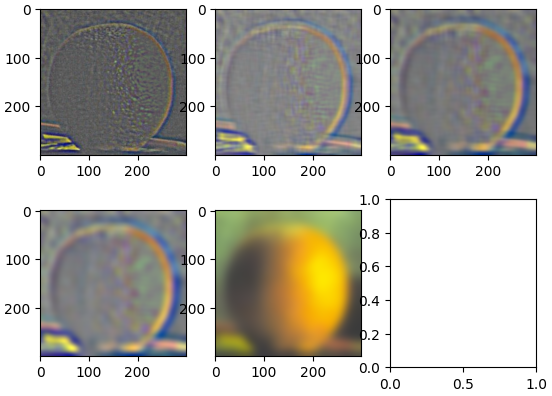
Combining into 1 Filter
One of the biggest advantages of using convolution over cross correlation is its commutative property. This allows us to combine both the gaussian blur and the difference operators into 1 singular convolution. If I do this using the finite difference operator and the gaussian filter, I get the following output which is the same as the 2 convolution output.